Dimension in the neural network
I would like to write some posts about neural networks. This one is first and we will focus on the dimensionality. It is a basic principle in the neural network (to have the right dimension in matrix/vector multiplication).
It is always good to use a piece of paper. You can sketch your neural network like this:
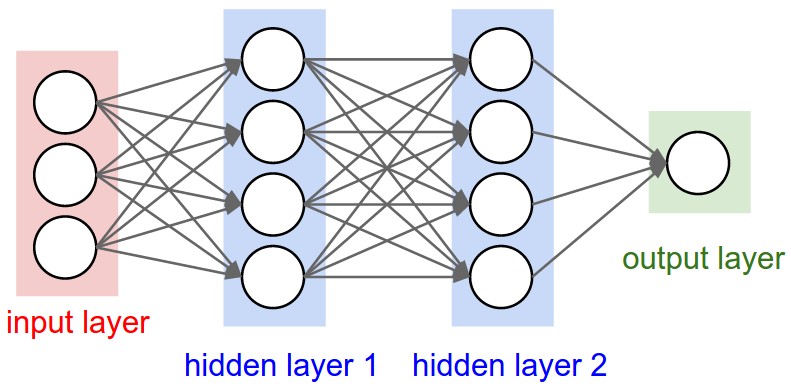
We should focus on the first layer (neurons in the red boxes):
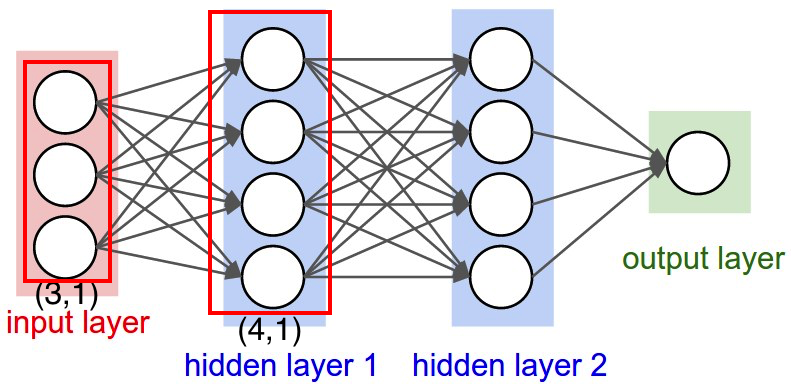
Here is what we know already from looking at picture
- To not confuse you, I write the dimension in this format \((row, column) \)
- Input is \((3, 1)\) - 3 input features
- Layer 1 state is \((4, 1)\) - 4 features
- Layer 1 activation is \((4, 1)\) - 4 activation features
We need to deduce weight and biasis.
\[ z = W * x + b \] \[ a = g(z) \]
so
\[(4,1) = (w1, w2) * (3,1) + (b1, b2)\] \[(4,1) = g((4,1)) \]
Last equation is sutisfied because our g funciton in general does not change dimensionality. To satisfy first equation we need some basic matrix calculus:
\[ (a, b) * (c, d) = (a, d) \]
if and only if b=c
I will recommend to look at the Wikipedia. Or just these two images:
Then it is obvious that:
\[(4, 1) = (w1, w2) * (3, 1) \]
if and only if w1 = 4 and w2 = 3
And \(b\) is obvious because it is basic addition of matrix, so result is:
\[(4, 1) = (4, 1) * (3, 1) + (4, 1)\]
Images are taken from CS231n.

